Submodual

子模态定义

子模态是集合函数的一种性质。一个集合函数$f(x)$的定义要满足下面这个性质

\begin{equation}f: 2^{\Omega}\rightarrow \mathbb{R}\end{equation}

即$f(x)$的定义域为集合$Ω$的任何一个子集，值域为实数集。而这个集合函数如果要满足子模态性质的话，还需要满足下面三个等价条件中的任何一个。

对于任何一个$X,Y\subset Ω$且$X\subset Y$，以及对任何一个$x\in Ω \\ Y$，下面的式子一定成立。
$$f(X\cup {x})-f(X)\geq f(Y\cup {x})-f(Y)$$
对于任何一个$X,Y\subset Ω$ ，下面的式子一定成立。
$$f(X)+f(Y)\geq f(X\cup Y)+f(X\cap Y)$$
对于任何一个$X\subset Ω$及$x_1 ,x_2 \in Ω∖X$，下面的式子一定成立,
$$f(X\cup {x_1})+f(X\cup {x_2})\geq f(X\cup {x_1,x_2})+f(X)$$

读者可以很轻松的验证这几个条件是等价的，这里就不去证明了。

根据这些条件，我们可以得出下面这个结论。设$f_1 (x),f_2 (x),\cdots,f_k (x)$都是有子模态性质的函数，$c_1 ,c_2 ,\cdots,c_k$ 是非负实数，则下面这个函数

\begin{equation}F(x)=\sum_{i=1}^{k}{c_if_i(x)}\end{equation}

仍然是子模态的。即多个子模态函数的非负线性组合仍然是子模态函数。这个推论可以很简单的验证出来，这里也就懒得做证明的。

子模态与贪心方法

接下来的问题就是，子模态这个函数性质有什么用。简单来说子模态这个函数性质在组合优化中很有用。特别是针对保持|x| 的大小固定，然后去求$f(x)$的最大值这种问题。这个子模态性质可以保证我们在贪心求解这个问题得到的解不会差，事实上贪心解$f(x)$的值不会小于$(1−1/e )*OPT$，其中$OPT$为最优解。在该问题的贪心求解过程中，我们是从$0$开始构建目标集合$x$的。每一步我们将一个新的元素加入到$x$中，迭代$k$步。我们以$X_i$ 来代表迭代$i$次之后的$x$集合，初始$x_0 =\emptyset$。我们对下一个要加入的节点$u$的选取的贪心规则为

\begin{equation}u=arg max_{u}{f(X_{i-1}\cup { u})}\end{equation}

现在我们要证明在此贪心规则下

\begin{equation}f(x)\geq (1-\frac{1}{e})*OPT\end{equation}

为此，我们先证明一个引理

\begin{equation} f(A\cup B)-f(A)\leq \sum_{j=1}^{k}{[f(A\cup {b_j})-f(A)]}\end{equation}

其中$B={b_1,\cdots,b_k}$.此时我们定义$Bi=b_1,\cdots,b_i$，则

\begin{equation}\begin{split}f(A\cup B)-f(A)&=\sum_{i=1}^{k}{[f(A\cup B_i)-f(A\cup B_{i-1})]}\\&=\sum_{i=1}^{k}{[f(A\cup B_{i-1}\cup {b_i})-f(A\cup B_{i-1})]}\\&\leq\sum_{j=1}^{k}{[f(A\cup {b_j})-f(A)]}\end{split}\end{equation}

设最优解为$T={t_1,\cdots,t_k}$,$\delta_i=f(X_i)-f(X_{i-1})$,根据上面这个不等式我们可以推出

\begin{equation}\begin{split}f(T)&\leq f(X_i\cup T)\\&=f(X_i\cup T)-f(X_i)+f(X_i)\\&\leq\sum_{j=1}^{k}{[f(X_i\cup {t_j})-f(X_i)]}+f(X_i)\\&\leq\sum_{j=1}^{k}{[\delta_{i+1}]}+f(X_i)\\&=f(X_i)+k\delta_{i+1}\end{split}\end{equation}

综上我们可以得出这个结论

\begin{equation}\delta_{i+1}\geq \frac{1}{k}[f(T)-f(X_i)]\end{equation}

所以

\begin{equation}\begin{split}f(X_{i+1})&=f(X_i)+\delta_{i+1}\\&\geq f(X_i)+\frac{1}{k}[f(T)-f(X_i)]\\&=(1-\frac{1}{k})f(X_i)+\frac{1}{k}f(T)\end{split}\end{equation}

通过上面的递推式，我们可以给出$f(X_i)$

\begin{equation}f(X_i)\geq [1-{(1-\frac{1}{k})}^i]f(T)\end{equation}

这个是简单的递推数列求通项，这里也就懒得证明了。所以

\begin{equation}f(X_k)\geq [1-{(1-\frac{1}{k})}^k]f(T)\geq [1-\frac{1}{e}]f(T)\end{equation}

这就是贪心大法好的证明。

子模态的应用

下面我就以影响最大化这个例子来说明这个东西还是有点用的。

影响最大化(influence maXimization)这个问题是定义在一个有向无环图$G=(V,E)$上的。对于这个图的任意一条边$(v,w)$，我们都有这条边的权值$p_{vw}$ 。$p_{vw}$ 用来代表$v$对$w$的影响能力，这个影响能力是一个概率，因此$p _{vw} \in [0,1]$。对于边$(v,w)$不存在的时候，$p_{vw}$ 定义为0.

发散网络

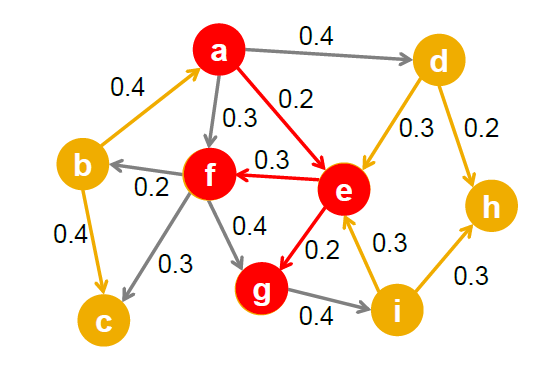
这个图类似于一个传播网络，或者感染网络。现在我们来定义影响函数$f(X)$，这是一个集合函数。为了表征这个函数，我们需要定义一个随机过程$S$。初始时刻0，我们给定输入$P=X_0$ ，$P$表示活动集合。在时刻$t$，我们对$\forall v \in X_t$做如下操作：$\forall w\in V/P$，我们以概率$p_{vw}$ 将节点$w$加入到$X_{t+1}$ 中。此操作完成之后，检查$X_{t+1}$ 是否为空。如果为空，则返回$P$；否则$P=P \cup X_{t+1}$ ，然后重复上面的操作。这个模型叫做independent Cascade Model，由Goldenberg, Libai,and Muller提出来的（这个模型是不是跟微博上的转发非常像）。

发散过程

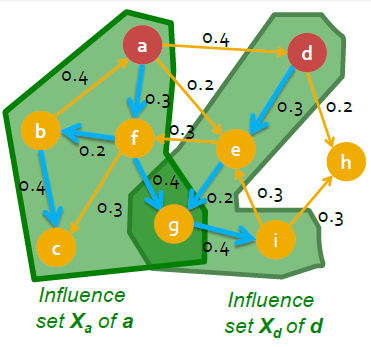
最后我们来表征$f(X)$，就是初始集合$X$该过程$S$下所返回的集合$P$的大小的平均值。

影响最大化问题就是在固定集合$X$大小$k$的情况下，最大化$f(X)$。我们可以证明这个优化问题是NPHard 的。该问题的简化形式为$p_{vw}$ 都是1，此时该问题不再是一个随机过程。每个初始点$v$的可达集是固定的，我们可以表示为$R_v$ 。因此，原问题等价于在集合$R_1 ,\cdots,R_{|v|}$ 中找到$k$个集合，使得

\begin{equation} arg\max_u{f(S_{i-1}\cup{u})}\end{equation}

但是，如何证明这个贪心是有效的一个难题，因为这是一个随机过程，每个点的增益在每一个时刻都是一个不同的随机变量，函数表达式也不是一个解析式。

我们现在先从简化问题出发，然后再去求解原问题。而简化问题就是我们之前提到的集合覆盖问题$f(S)=|\cup i\in S x_i |$，这个问题其实是子模态的。证明也很简单，直接对集合进行分割就行了，这里就省去了具体的证明。我们再回归到原问题，在$t$时刻节点$v$引发$w$的概率为$p_{vw}$ ，这是一个$01$分布。事实上这个结果是$0$还是$1$与时刻$t$是无关的，所以我们可以预先生成好这个随机变量。对所有的边进行提前生成随机变量之后，我们就得到了一个图$N$.$N$的拓扑结构与原图一致，不同的地方就是$p_{vw}$ 。

新图1

新图2

新图3

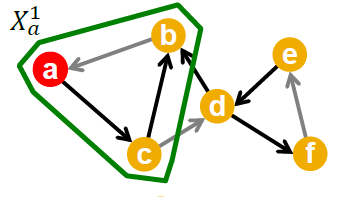
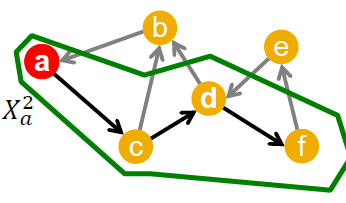
而当$v$引发$w$时，$p_{vw} =1$，否则就等于0.在$N$中的影响最大等价于之前讨论的集合覆盖问题。设生成图$N_i$ 的概率为$p_i$ ，设$f_i(X)$为在图$N_i$ 上寻找影响最大的解，则

\begin{equation}f(X)=\sum_{i=1}{p_if_i(X)}\end{equation}

可以看出这是多个子模态函数的非负线性组合，因此$f(X)$是子模态的。又根据我们在之前证明贪心法在子模态函数上是可行的，所以贪心法对影响最大问题是可行的。

参考链接

http://en.wikipedia.org/wiki/Submodular 维基百科上的介绍
http://www.cs.cornell.edu/home/kleinber/kdd03-inf.pdf 业界大佬kleinberg ，请收下我的膝盖。